Кривая дракона
Построение кривой драконаСкладывание бумажной полоскиОдин из способов построения кривой дракона - складывание длинной бумажной полоски. Начнем с горизонтальной полоски: согнем вверх ее правую половину и наложим на левую. Затем сложим полученную двойную полоску так, чтобы перегиб, расположенный ранее справа, совпал с левым краем сложенной полоски; повторим этот процесс столько раз, сколько сможем. (Практически это вряд ли удастся сделать больше семи раз, но теоретически процесс можно продолжать до бесконечности). Если после этого бумагу развернуть, то на ней получится интересная последовательность сгибов. Обозначим обращенный вверх сгиб через U, а обращенный вниз сгиб - через D. Тогда начало последовательности выглядит так: ÛÛDÛUDDÛUUDDUDDÛUUDUUDDDUUDDUDDÛU Первый, второй, четвертый, восьмой и т.д. сгибы, отмеченные символом ˆ, назовем "наружными". Легко видеть, что сгиб, находящийся на k шагов впереди наружного, всегда направлен противоположно сгибу, расположенному на k шагов позади. Это свойство вместе с тем фактом, что наружными могут быть только сгибы U (потому что полоску складывали только вверх), определяет правило, позволяющее выписать сколько угодно членов этой последовательности. Существуют и другие, эквивалентные правила. Например, если n = 2kq, где q нечетно, то n-ый сгиб есть U или D в зависимости от того, сравнимо ли q по модулю 4 с 1 или с 3. Далее поставим полоску вертикально и согнем бумагу на 90° в каждом сгибе в направлении этого сгиба. Получим кривую дракона. Если 3 раза повернуть полученный узор на четверть оборота (на 90°) вокруг его начальной точки, т.е. из одной и той же точки построить хвостом к хвосту четырех драконов, то они нигде не пересекутся. 






Соединим начальную точку со второй вершиной кривой дракона, вторую - с четвертой и т.д. В результате получится копия исходного узора, только увеличенная в √2 раз и повернутая на 45° по часовой стрелке. Отсюда видно, что наружные сгибы принадлежат логарифмической спирали с полюсом в начальной точке кривой. Исследовано много вариантов складывания. Вероятно, самым простым из них является складывание, при котором вместо того, чтобы сгибать полоску всегда вверх, ее сгибают поочередно то вверх, то вниз. Тогда в последовательности сгибов наружными оказываются то U, то D, но правило, связанное с наружными сгибами, сохраняется: k-ый сгиб после наружного сгиба всегда направлен противоположно k-ому сгибу, предшествующему ему. Это вариант складывания представлен на следующих двух рисунках. На левом рисунке показан узор, который получается после развертывания сложенной таким образом полоски и многократного сгибания ее, но не на углы в 90°, а на углы в 108°. Весь получаемый таким образом узор умещается в бесконечном секторе с углом 36°. Наружные сгибы лежат поочередно то на правой, то на левой границе сектора. Если согнуть полоску еще немного, уменьшив углы до 90°, получится не имеющий самопересечений маршрут, показанный на правом рисунке. На рисунке уголки закруглены, чтобы было лучше видно, как проходит этот путь. 
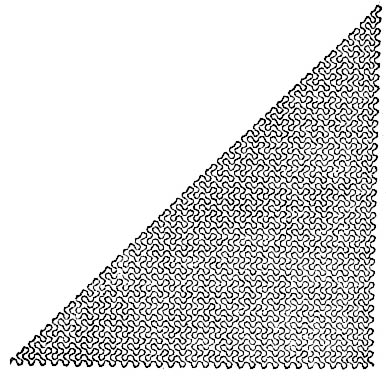
Построение кривой дракона с помощью последовательности двоичных цифрКаждую кривую дракона можно описать с помощью последовательности двоичных цифр, где 1 соответствует повороту налево, а 0 — повороту направо (кривая вычерчивается на листе бумаги от хвоста к пасти дракона). Формула для кривой дракона любого порядка (большего 1) получается с помощью следующего рекуррентного метода. К формуле кривой дракона предыдущего порядка мы справа приписываем единицу. Это дает нам половину формулы. Затем мы отыскиваем в наборе двоичных цифр, предшествующих приписанной единице, центральную единицу и заменяем ее на нуль, после чего приписываем то, что получилось, справа от уже построенной половины формулы. Кривая дракона первого порядка имеет двоичную формулу 1. Приписав справа единицу, получим 11. Единственная цифра, стоящая перед приписанной единицей, является "центральной". Заменив ее на 0 и приписав его справа, получаем двоичную формулу кривой дракона второго порядка: 110. Чтобы получить формулу кривой дракона третьего порядка, приписываем к 110 справа 1 и, изменив центральную цифру числа 110 с 1 на 0, повторяем его справа от 1101: 1 101 100. Аналогично получаются формулы для кривых дракона более высокого порядка. Нетрудно видеть, что кривая дракона n-го порядка (n > 1) состоит из двух экземпляров кривых дракона (n—1)-го порядка, соединенных "головой к голове", в силу чего вторая кривая вычерчивается "наоборот": не от хвоста к голове, а от головы к хвосту. Формулы кривых дракона с 1 до 6 порядка:
Получение кривой дракона с помощью геометрического построенияБенкс придумал способ, позволяющий получать кривые дракона с помощью геометрического построения. Сначала берется отрезок единичной длины. Затем он заменяется на два отрезка, образующих боковые строны равнобедренного прямоугольного треугольника, для которых исходный отрезок является гипотенузой. В результате отрезок как бы прогибается под прямым углом. Направление прогиба чередуется. Первый отрезок прогибается вправо (по ходу движения слева направо), второй – влево, третий – опять вправо и т.д. Таким образом, после каждого шага число имеющихся отрезков удваивается, а длина каждого соответственно уменьшается в √2 раз. 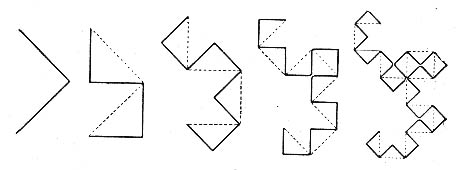
Программа построения кривой дракона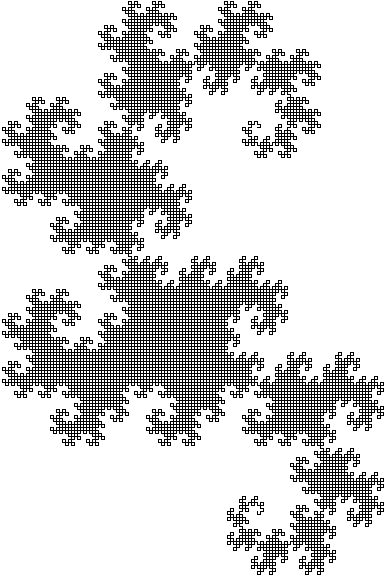
Program Dragon;
Uses Graph, Crt;
Const
c = 1024*16;
d = 3;
da =pi/2;
Var
i: Integer;
gd, gm: Integer;
a,x,y : Real;
procedure lineto1(x,y,l,u:real);
begin
line(Round(x),round(y),round(x+l*cos(u)),
Round(y-l*sin(u)));
end;
function f(n:integer):integer;
Label
nach;
Var
j:integer;
Begin
j:=n;
nach:
if (j-1) mod 4 = 0 then f:=-1
else if (j-3) mod 4 = 0 then f:=1
else Begin
j:=j div 2;
goto nach;
End;
End;
Begin
gd:=Detect;
InitGraph(gd,gm,'f:\tp7\bgi'); {указан путь к файлам *.BGI}
x:=150;
y:=150;
a:=pi/2;
For i:=1 to c+1 do Begin
lineto1(x,y,d,a);
x:=x+d*cos(a);
y:=y-d*sin(a);
a:=a-da*f(i);
End;
Readkey;
CloseGraph;
end.
Еще одна программа построения кривой дракона
program dragon;
uses graph, crt;
var gd,gm,k:integer;
procedure st(x1,y1,x2,y2,k:integer);
var xn,yn:integer;
begin
if (k>0)and(not keypressed) then {условие выхода}
begin
xn:=(x1+x2)div 2+(y2-y1)div 2; {уравнение для Х и У координаты конца нового отрезка}
yn:=(y1+y2) div 2-(x2-x1) div 2;
st(x2,y2,xn,yn,k-1);
st(x1,y1,xn,yn,k-1);
end
else
line(x1,y1,x2,y2);
end;
begin
gd:=detect;
initgraph(gd,gm,'f:\tp7\bgi'); {указан путь к файлам *.BGI}
k:=20;
setcolor(red);
setbkcolor(7);
st(200,200,500,300,k);
readln;
end.
Источники: См. также: |
