Золотое сечениеЕсли разделить любой отрезок на две части так, чтобы отношение большей части отрезка к целому было равно отношению меньшей части к большей, получим сечение, которое называют золотым.
На рисунке отрезок АВ разделен точкой С так, что АС : АВ = СВ : АС. Обозначим это отношение Ф. Если принять длину отрезка АВ за a, а большую часть отрезка (АС) за b, то a:b = b:(a-b), или a2-ab-b2=0. Разделив обе части уравнения на b2 и обозначив искомое отношение a/b буквой Ф, получим уравнение:
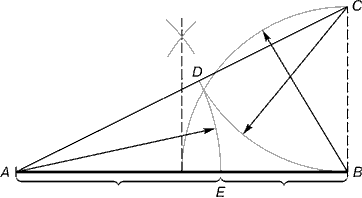
Ф2-Ф-1=0. (*), или Ф2 = Ф+1. (**) Нетрудно заметить, что взаимно обратные величины 0,618... и 1,618... отличаются только первой цифрой. Этот факт заложен в самом уравнении для числа Ф (**). Разделим обе его части на Ф: Если извлечь квадратный корень из обеих частей уравнения Ф2 = Ф+1, получим Ф=√(1+Ф); если заменять под корнем величину Ф на вычисленное значение (бесконечно продолжая этот процесс), получим: Поскольку Ф = 1 + 1/Ф, можно в выражении в правой части равенства заменить в знаменателе дроби Ф на 1 + 1/Ф. Выполняя это действие снова и снова, мы получим еще одно выражение для числа Ф: 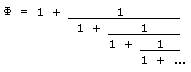 Эти числа получили название "золотых". Они действительно замечательные. Везде, где человек ощущает гармонию - в звуках, в цвете, в размерах, - всюду присутствует "Золотое число". Глаз радуется отрезку, разделенному не строго пополам, а именно в пропорции 0,618:0,382. Может, поэтому так часто находят золотое сечение в памятниках античной архитектуры, в пропорциях идеальных человеческих фигур, вылепленных великими Фидием и Поликлетом, в классических музыкальных произведениях (еще пифагорейцы заметили, что музыкальный звукоряд построен по закону частот, равных "золотому числу"), живописи, поэзии, формах скрипок Страдивари, а также в природе – химии, ботанике, зоологии... Золотое сечение можно найти, рассматривая некоторые геометрические фигуры. Пятиконечная звезда, получаемая при последовательном соединении через одну всех вершин правильного пятиугольника (пентаграмма), всегда привлекала внимание людей совершенством формы. Пифагорейцы именно ее выбрали символом своего союза. В этой фигуре наблюдается удивительное постоянство отношений составляющих ее отрезков. 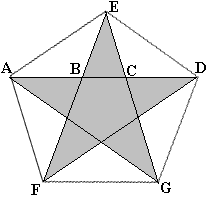 На рисунке AD:AC = AC:CD = AB:BC = AD:AE = AE:EC. Пользуясь симметрией звезды, этот ряд равенств можно продолжить. Все эти отношения равны числу Ф (1,618...). Для того, чтобы разделить отрезок АВ в "золотом" отношении, достаточно выполнить следующие построения с помощью циркуля и линейки:
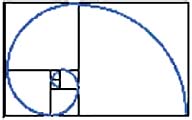
 Соразмерность, выражаемая числом Ф, по свидетельству многих исследователей, наиболее приятна для глаза. Леонардо да Винчи считал, что идеальные пропорции человеческого тела должны быть связаны с числом Ф. Именно он назвал деление отрезка в отношении Ф золотым сечением. Этот термин сохранился до наших дней. В эпоху Возрождения золотое сечение было очень популярно среди художников, скульпторов и архитекторов. Например, в большинстве живописных пейзажей линия горизонта делит полотно по высоте в отношении, близком к Ф. А выбирая размеры самой картины, старались, чтобы отношение ширины к высоте тоже равнялось Ф. Такой прямоугольник стали называть "золотым". Для построения "золотого прямоугольника" в качестве смежных сторон возьмем длины сторон АВ и АК треугольника АВК. 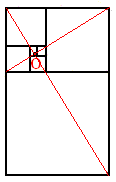 Бывает и "золотой треугольник". На рисунке с пентаграммой это равнобедренные треугольники FEG, EAC, BEC, у которых отношение длины боковой стороны к длине основания равняется Ф. Одно из замечательных свойств такого треугольника состоит в том, что длины биссектрис углов при его основании равны длине самого основания. 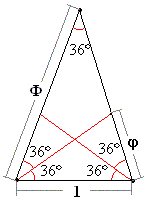 Есть и "золотой кубоид" - это прямоугольный параллелепипед с ребрами Ф (1,618...), 1 и ф (0,618...). Площадь его поверхности равна 4Ф, а диагональ - 2. Отсюда следует, что описанная вокруг него сфера имеет радиус 1, и, значит, ее площадь равна 4p. Поэтому отношение поверхности этой сферы к поверхности "золотого кубоида" равно p:Ф. Представление о золотом сечении и "золотых" фигурах будет неполным, если не сказать о спирали. Если посмотреть на раковину улитки, можно заметить, что она закручена по очень красивой спирали, которая близка к так называемой логарифмической спирали. Логарифмическая спираль в полярных координатах описывается уравнением r=aw, где r - расстояние от точки до полюса, w - угол поворота, a - некоторая константа. Графическое приближение "золотой спирали" можно построить, соединив дугами точки квадратов, отсеченных от золотого прямоугольника при построении новых золотых прямоугольников. 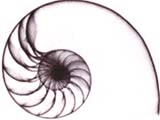
Где мы можем столкнуться с золотым сечением?
Золотое сечение в архитектуре, скульптуре, живописи, фотографии Источники: |