Растрепанный Блокнот | Числа Фибоначчи и золотое сечение

Золотое сечение

(См. также: Понятие золотого сечения
Золотое сечение в архитектуре, скульптуре, живописи, фотографии
Золотое сечение в живой природе
Золотые пропорции в литературе. Поэзия и золотое сечение
Золотое сечение в музыке, физике, астрономии. Золотое сечение и восприятие изображений (право- и левополушарные люди))

Числа Фибоначчи и золотое сечение

Одним из наиболее известных математиков эпохи Средневековья по праву считается Леонардо Фибоначчи. По иронии судьбы Фибоначчи, который внес выдающийся вклад в развитие математики, стал известным в современной математике только лишь как автор интересной числовой последовательности, называемой числами Фибоначчи. Эта числовая последовательность была получена Фибоначчи при решении знаменитой "задачи о размножении кроликов". Формулировка и решение этой задачи считается основным вкладом Фибоначчи в развитие комбинаторики. Именно с помощью этой задачи Фибоначчи предвосхитил метод рекуррентных соотношений, который считается одним из мощных методов решения комбинаторных задач. Рекуррентная формула, полученная Фибоначчи при решении этой задачи, считается первой в истории математики рекуррентной формулой.

Сущность своей "задачи о размножении кроликов" Фибоначчи сформулировал предельно просто:

"Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения?"

Месяц	Количество взрослых пар	Кол-во новорожденных пар	Общее кол-во пар
1	1	0	1
2	1	1	2
3	2	1	3
4	3	2	5
5	5	3	8
6	8	5	13

Изучая последовательности чисел, обозначающих количество пар кроликов, можно установить следующую закономерность в этих числовых последовательностях: каждый член последовательности, начиная с некоторого номера, равен сумме двух предыдущих. Если теперь обозначить n-й член последовательности, удовлетворяющей этому правилу через Fn, тогда указанное выше общее правило может быть записано в виде следующей математической формулы:

F_n = F_n-1 + F_n-2.

Такая формула называется рекуррентной формулой.

В математике под числами Фибоначчи, как правило, понимается числовая последовательность:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...

Если в ряду чисел Фибоначчи взять отношение последущего члена к предыдущему или наоборот, то получим уже знакомые нам числа: 1,618 и 0,618. Причем, чем больше порядковые номера членов, тем точнее выполняется "золотое" соотношение.

Числа Фибоначчи U_k	Отношение х=U_k/U_k-1	x-Ф
1
1	1,0000000000	-0,6180339887
2	2,0000000000	0,3819660113
3	1,5000000000	-0,1180339887
5	1,6666666667	0,0486326779
8	1,6000000000	-0,0180339887
13	1,6250000000	0,0069660113
21	1,6153846154	-0,0026493734
34	1,6190476190	0,0010136303
55	1,6176470588	-0,0003869299
89	1,6181818182	0,0001478294
144	1,6179775281	-0,0000564607
233	1,6180555556	0,0000215668
377	1,6180257511	-0,0000082377
610	1,6180371353	0,0000031465
987	1,6180327869	-0,0000012019
1597	1,6180344478	0,0000004591
2584	1,6180338134	-0,0000001753
4181	1,6180340557	0,0000000670
6765	1,6180339632	-0,0000000256
10946	1,6180339985	0,0000000098
17711	1,6180339850	-0,0000000037
28657	1,6180339902	0,0000000014
46368	1,6180339882	-0,0000000005
75025	1,6180339890	0,0000000002
121393	1,6180339887	-0,0000000001

Кроме того, n-я степень числа Ф выражается замечательной формулой:

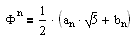
где a_n - n-ое число Фибоначчи, а b_n - n-ый член последовательности 1, 3, 4, 7, 11, 18, 29, ..., строящейся по тому же принципу, что и последовательность Фибоначчи.

	На главную страницу

	Все тексты раздела