Сапог Шварца

В 1890 г. немецкий математик Герман Шварц придумал конструкцию, позже названную "сапогом Шварца". Вы видите ее на рисунке: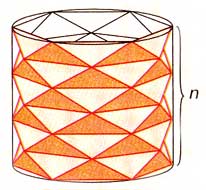

Высота цилиндра делится плоскостями, параллельными основаниям, на n равных частей. В образовавшиеся сечения (окружности) вписываются правильные k-угольники, причём соседние k-угольники повёрнуты относительно друг друга на угол 180 °/k. Затем вершины k-угольников соединяются так, что образуется поверхность из 2nk треугольников; каждый её "слой" — антипризма. Если n, k ® ¥, то размеры этих треугольников становятся сколь угодно малыми. С увеличением k наши k-угольники всё плотнее прижимаются к их описанным окружностям, а вся поверхность — к цилиндру. Можно ожидать, что при п, k ® ¥ её площадь, т. е. сумма площадей всех треугольных граней, стремится к боковой поверхности цилиндра. Но это совершенно не так!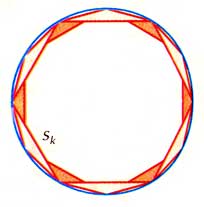
Посмотрим на Шварцев "сапог" сверху:

Проекция каждой его грани на основание цилиндра — это треугольник, образованный стороной k-угольника и серединой стягиваемой ею дуги окружности. Его площадь зависит только от k; обозначим её s_k. Поскольку площадь при проекции может только уменьшиться, полная поверхность "сапога" B(n,k) не меньше 2nk·s_k. Теперь для каждого k возьмём такое n=n(k), зависящее от k, что n(k)·s_k > 1. При этом выборе n площадь B(n,k) > 2k, т. е. неограниченно возрастает при k ® ¥. Поверхность, как настоящий сапог, собирается частыми складками. Более того, можно выбрать такую последовательность n(k), чтобы площади соответствующих многогранных поверхностей сходились к любому (!) заданному числу, не меньшему боковой поверхности цилиндра.

Этот пример демонстрирует те подвохи, которых нужно избежать, давая определение площади поверхности через приближение многогранниками.

Вы можете изготовить модель "сапога Шварца". Разлинуйте прямоугольник из плотной бумаги с одной стороны на ромбы (по красным линиям на рис. 3), а с другой — на горизонтальные полосы (по синим линиям).

Прочертите бумагу по этим линиям тупой стороной ножа. А теперь просто сверните лист в трубку, слегка надавливая на центры красных ромбов, чтобы он лучше складывался по линиям, и склейте противоположные стороны прямоугольника.

Источник: Энциклопедия для детей. Т.11. Математика. - М.: Аванта+, 1998. Стр. 366