Вращающиеся кольца тетраэдров

По материалам книги: У. Болл, Г. Коксетер. Математические эссе и развлечения. Пер. с англ. - М.: "Мир", 1986. - 474 с. с ил.
Стр. 168-169

Дж.М. Андреас и Р.М. Сталкер независимо друг от друга открыли семейство изгибаемых конечных многогранников с 2n вершинами, 6n ребрами (из которых 2n сдвоенных) и 4n треугольными гранями; n может равняться 6, 8 или любому большему целому числу. Гранями служат грани n тетраэдров, соединенных между собой в циклическом порядке по определенным парам противоположных ребер каждого, так что получается фигура наподобие кольца. При n = 6 эта фигура еще достаточно жесткая, но при n = 8 она уже может изгибаться и выворачиваться до бесконечности, как колечко дыма. Когда n четно, фигура стремится принять симметричную форму; особенно хороша она при n = 10. Когда n нечетно, из-за полного отсутствия симметрии картина становится, пожалуй, еще более захватывающей. При n, большем или равном 22, кольцо может заузливаться.

Для изготовления модели такого кольца достаточно одного листа бумаги. В случае n=6 скопируйте приведенную здесь диаграмму:

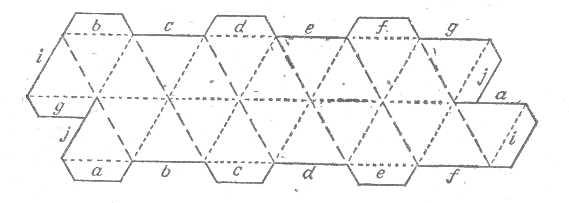
Вырежьте ее, сделайте сгибы по внутренним линиям - по штриховым линиям вверх, а по пунктирным вниз - и приклейте клапаны в соответствии с буквенными обозначениями (в случае, когда n кратно 4, концы соединяются несколько иначе).

При n=6 должно получиться нечто вроде:

На рисунке - модель перед склеиванием, клапаны прилегают неплотно. Это сделано намеренно, чтобы проиллюстрировать способ складывания. После склеивания получается очень аккуратная моделька. Единственный этап, на котором могут возникнуть трудности, - приклеивание клапанов последнего тетраэдра (половина которого находится на одном конце развертки, а половина - на другом). Остальные тетраэдры складываются почти автоматически, если аккуратно согнуть развертку по всем линиям еще до начала складывания.

Поскольку у такого многогранника два типа ребер, он неправильный, и вместо равносторонних треугольников можно рассматривать равнобедренные. Сделав двойные ребра достаточно короткими по сравнению с остальными ребрами, можно добиться того, что и при n=6 кольцо удастся полностью вывернуть.

На мой взгляд, самое красивое кольцо получается все же при n=10: при взгляде на кольцо сверху видна очень аккуратная звезда с пятью лучами; это не обязательно правильная пентаграмма, все зависит от того, в каком положении находится кольцо тетраэдров. При увеличении числа тетраэдров в кольце оно становится менее жестким, и симметрия частично теряется даже при четных n.